Equações e Inequações

Equações e inequações são nomes bem parecidos, porém, isso não significa que tenham significados semelhantes. 

Quando escrevemos uma equação, estamos criando uma igualdade, e por esse motivo, o sinal de igual ( = ) sempre deve aparecer em nossa expressão. Além disso, em uma equação, nosso objetivo é encontrar um ou mais números específicos que satisfaçam nossa expressão matemática. Portanto, em uma equação, uma coisa deve ser obrigatoriamente igual a outra, ou isso não será uma equação.

Já em uma inequação, estamos falando sobre uma desigualdade, e dessa forma, teremos os sinais de maior ( > ), menor ( < ), maior ou igual ( ≥ ) e menor ou igual ( ≤ ) em nossa expressão. O nosso objetivo agora não é encontrar um número específico, mas sim um conjunto de valores que satisfaçam nossa condição de desigualdade. As resoluções das inequações são praticamente iguais às das equações, exceto quando há mais de 1 resposta. Neste caso, você deverá avaliar quais das respostas fazem parte do conjunto solução, como veremos mais à frente.

Inequações quociente

Vamos agora ver algumas inequações onde temos a incógnita no denominador da fração. Um ponto importante sobre essas expressões é a sua condição de existência. Em inequações quociente, o denominador na fração nunca pode ser igual a zero. Então é necessário atentar-se aos resultados encontrados. Vamos ver como resolvê-las!

Inequação 1: 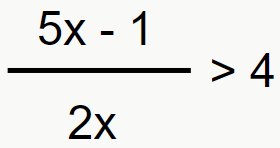inequação quociente

Para começar, podemos resolver como uma inequação de primeiro grau.

5x -1 > 2x * 4

5x – 1 > 8x

-3x > 1

x > -⅓

Então é isso? Para que \( \frac{5x-1}{2x} \) seja maior que 4, x deve ser maior que \( -\frac{1}{3} \)? Lembra que há pouco foi dito que você deve verificar se há algum valor que quebre a condição de “não 0 no denominador”? Sendo assim, perceba que, no caso da nossa expressão, se substituirmos x = 0, o denominador fica igual a 0, ou seja, o zero não pode fazer parte do nosso conjunto de soluções. Nesse caso, devemos analisar também o que acontece com a expressão quando avaliada em valores maiores e menores que 0.
Lembrando que já temos a restrição do \( -\frac{1}{3} \), pois x deve ser maior que \( -\frac{1}{3} \). Desse modo, então temos que pegar um valor que é menor que 0 e maior que e \( -\frac{1}{3} \), e outro valor maior que 0.

Vamos escolher -1/4 e 1:

\[ \frac{5*(-\frac{1}{4})-1}{2*(-\frac{1}{4})} = 4,5 \]
\[ \frac{(5*1)-1}{2*1} = 2 \]
Como 4,5 é maior que 4, então é possível concluir que números entre \( -\frac{1}{3} \) e 0 fazem parte da solução. No entanto, como 2 é menor que 4, então números maiores que 0 não fazem parte da solução. Portanto, nosso conjunto solução é \( -\frac{1}{3} < x < 0 \).
<– Equações racionais
Equações irracionais –>

Referências

Inequações quociente

https://mundoeducacao.uol.com.br/matematica/inequacao-quociente.htm

Pular para o conteúdo